In the diagram above, O is the center of the circle, |SQ|...
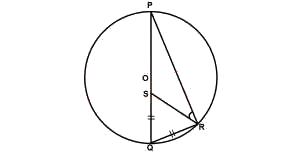
In the diagram above, O is the center of the circle, |SQ| = |QR| and ∠PQR = 68°. Calculate ∠PRS
34o
45o
56o
62o
68o
Correct answer is A
From the figure, < PQR = 68°
∴ < QRS = < QSR = 180−682 (base angles of an isos. triangle)
= 56°
∴ < PRS = 90° - 56° = 34° (angles in a semi-circle)
Similar Questions
How many different 8 letter words are possible using the letters of the word SYLLABUS? ...
In the diagram, O is the center of the circle and the reflex angle ROS is 264o. Find ∠RTS...
Calculate the distance between points L(-1, -6) and M(-3, -5)...
If the exterior angles of quadrilateral are yo, (y + 5)o, (y + 10)o and (y + 25)o, find y...
Given that log3 27 = 2x + 1, find the value of x....
In the diagram PQ is a diameter of circle PMQN center O, if ∠PQM = 63o, find ∠MNQ...