In the diagram, POS and ROT are straight lines. OPQR is a...
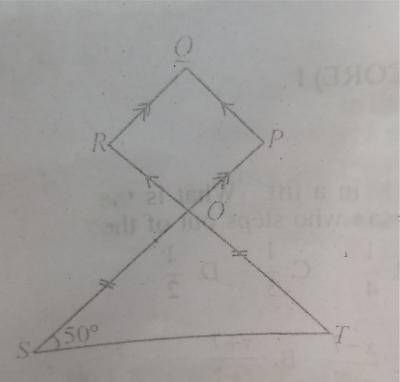
In the diagram, POS and ROT are straight lines. OPQR is a parallelogram, |OS| = |OT| and ∠OST = 50°. Calculate the value of ∠OPQ.
100\(^o\)
120\(^o\)
140\(^o\)
160\(^o\)
Correct answer is A
S\(O\)T = 180\(^o\) - (50 + 50)
= 80\(^o\)
P\(Q\)R = 80\(^o\)
= \(\frac{360^o - 160^o}{2}\) = 100\(^o\)
Similar Questions
Find the area of the shaded portion of the semicircular figure. ...
Find the number of term in the Arithmetic Progression(A.P) 2, -9, -20,...-141. ...
The angle of elevation of the top T of a pole from a point X on the horizontal ground is 32°, if...
Solve the equation \( 3x^2 − 4x − 5 = 0 \)...
Determine the value of x for which (x\(^2\) - 1) > 0? ...
For what values of y is the expression \(\frac{6y-1}{y^2 - y-6}\)...
What is the solution of \(\frac{x - 5}{x + 3} < -1\)?...
In the diagram, \(\overline{PU}\)/\(\overline{SR}\), \(\overline{PS}\)/\(\overline{TR}\), ...