The graph is that of y = 2x2 - 5x - 3. For what v...
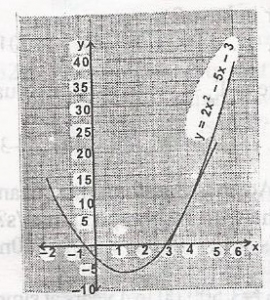
The graph is that of y = 2x2 - 5x - 3. For what value of x will y be negative? For what value of x will y be negative?
A.
-12≤x < 3
B.
-12<x≤3
C.
-12<x<3
D.
-12≤x≤3
Correct answer is C
2x2 - 5x - 3 = 0
2x2 - 6x + x - 3 = 0
2x(x - 3) + 1(x - 3) = 0
(2x + 1)(x - 3) = 0
2x + 1 = 0
2x = -1
x = -12
x - 3 = 0
-12 < x < 3
Similar Questions
Find the range of values of x for whichx+24−x+13>12...
Evaluate log1025+log1032−log108...
The nth term of a sequence is n2 - 6n - 4. Find the sum of the 3rd and 4th terms....
What value of g will make the expression 4x2 - 18xy + g a perfect square? ...
The sum 110112, 11112 and 10m10n02. Find the value of m and n. ...
If the diagram is the graph of y = x2, the shaded area is...
The following are scores obtained by some students in a test, Find the mode of the distribution...