In the diagram, O is the centre of the circle and PQ is a...
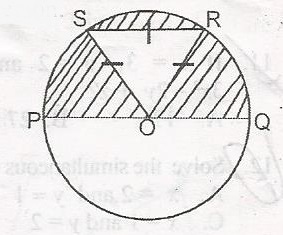
In the diagram, O is the centre of the circle and PQ is a diameter. Triangle RSO is an equilateral triangle of side 4cm. Find the area of the shaded region
43.36cm2
32.072
18.212
6.932
Correct answer is C
Area of shaded portion = Area of semicircle
Area of △ RSO
Area of semicircle = πr22=22×4×47×2
= 25.14cm2; Area of △RSO
=√s(s−1)(s−b)(s−c); where
s = a+b+c2
s = 4+4+42
= 6cm
= √6(6−4)(6−4)(6−4)
= √6(2)(2)(2)
= √18 = 6.93cm2
Area of shaded region
= 25.14 - 6.93
= 18.21cm2
Similar Questions
The diagram is a circle centre O. Find the value of x ...
What is the derivative of t2 sin (3t - 5) with respect to t? ...
In the diagram, QTR is a straight line and < PQT = 30o. find the sin of < PTR...
If sec2 θ + tan2 θ = 3, then the angle θ is equal to...
In △XYZ, XY = 3cm, XZ = 5cm and YZ = 7cm. If the bisector of XYZ meets XZ at W, wha...