find the length XZ in the triangle
...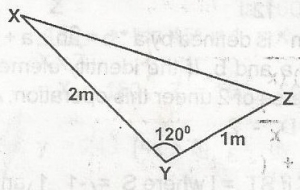
find the length XZ in the triangle
\(\sqrt{7m}\)
\(\sqrt{6m}\)
\(\sqrt{5m}\)
\(\sqrt{3m}\)
Correct answer is A
xz2 = xy2 + yx2 - 2(xy) (yz) cos 120o
= 22 + 12 - 2(2) (1) cos 1202
= 4 + 1 - 4x - cos 60 = 5 - 4x - \(\frac{1}{2}\)
5 + 2 = 7
xz = \(\sqrt{7}\)m
Similar Questions
Calculate the volume of the regular three dimensional figure drawn above, where < ABC = 90° (...
In the diagram above, AO is perpendicular to OB. Find x...
How many pupils took the test? ...
A school girl spends \(\frac{1}{4}\) of her pocket money on books and \(\frac{1}{3}\) on dress....
If dy/dx = 2x - 3 and y = 3 when x = 0, find y in terms of x. ...
If \(\left(\frac{1}{4}\right)^{(2-y)} = 1\), find y....
The shaded area represents ...
Find the matrix A A \(\begin {bmatrix} 0 & 1\\2 & -1 \end {bmatrix}\) = \(\begin {bmat...