In the figure, STQ = SRP, PT = TQ = 6cm and QS = 5cm. Fin...
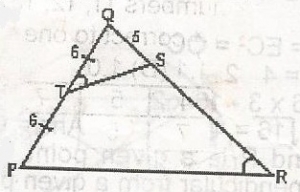
In the figure, STQ = SRP, PT = TQ = 6cm and QS = 5cm. Find SR
A.
\(\frac{47}{5}\)
B.
5
C.
\(\frac{32}{5}\)
D.
\(\frac{22}{5}\)
Correct answer is A
From similar triangle, \(\frac{QS}{QP} = \frac{TQ}{QR} = \frac{5}{12} = \frac{6}{QR}\)
QT = \(\frac{6 \times 12}{5} = \frac{72}{5} = SR = QR - QS\)
= \(\frac{72}{5} - 5 = \frac{72 - 25}{5}\)
= \(\frac{47}{5}\)
Similar Questions
Solve the simultaneous equations 2x - 3y = -10, 10x - 6y = -5...
In a triangle XYZ, < YXZ = 44° and < XYZ = 112°. Calculate the acute angle b...
In the diagram, |QR| = 5cm, PQR = 60<sup>o</sup> and PSR = 45<sup>o</sup>. F...
Find p, q for which \(\begin{pmatrix} 2p & 8 \\ 3 & -5q \end{pmatrix}\)\(\begin{pmatrix} 1 \...