Home / Aptitude Tests / Mathematics / In the figure, PQ is...

In the figure, PQ is the tangent from P to the circle QRS wi...

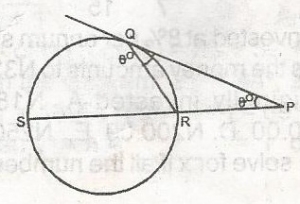
$In the figure, PQ is the tangent from P to the circle QRS with SR as its diameter. If QRS = $\theta$oand RQP = $\phi$o, which of the following relationships between $\theta$o and $\phi$o is correct$

In the figure, PQ is the tangent from P to the circle QRS with SR as its diameter. If QRS = $\theta$ ^oand RQP = $\phi$ ^o, which of the following relationships between $\theta$ ^o and $\phi$ ^o is correct

$\theta$ ^o + $\phi$ ^o = 90²

$\phi$ ^o = 90² - 2 $\theta$ ^o

$\theta$ ^o = $\phi$ ^o

$\phi$ ^o = 2 $\theta$ ^o

$\theta$ ^o + 2 $\phi$ ^o

View answer & explanation

Correct answer is E

180 - $\phi$ ^o = $\theta$ ^o + $\phi$ ^o (Sum of opposite interior angle equal to its exterior angle)

180 = 2 $\phi$ + $\theta$ ^o

See all Mathematics questions & answers

See more JAMB questions & answers

Aptitude Tests

Situational Judgement Questions and Answers

Personality Test

Verbal Reasoning Questions and Answers

Numerical Reasoning Questions and Answers

Typing Speed and Accuracy Test

Spatial Reasoning Questions and Answers

Logical Reasoning Questions and Answers

Data Interpretation Questions and Answers

Quantitative Reasoning Questions and Answers

Puzzles Questions and Answers

Abstract Reasoning Questions and Answers

Nigeria General Knowledge Questions and Answers

Microsoft Office Questions and Answers

See all →

View latest jobs in Nigeria today

In the figure, PQ is the tangent from P to the circle QRS with SR as its diameter. If QRS = θ\thetaoand RQP = ϕ\phio, which of the following relationships between θ\thetao and ϕ\phio is correct

Similar Questions

Aptitude Tests

In the figure, PQ is the tangent from P to the circle QRS with SR as its diameter. If QRS = $\theta$ ^oand RQP = $\phi$ ^o, which of the following relationships between $\theta$ ^o and $\phi$ ^o is correct