In the diagram, |QR| = 10cm, PR⊥QS, angle PSR = 30&d...
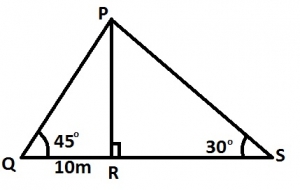
In the diagram, |QR| = 10cm, PR⊥QS, angle PSR = 30° and angle PQR = 45°. Calculate in meters |QS|
\(10(1+\sqrt{3})\)
\(20\sqrt{3}\)
\(10\sqrt{3}\)
\((10+\sqrt{3})\)
Correct answer is A
In \(\Delta\) PQR,
\(\tan 45 = \frac{PR}{10} \implies PR = 10 \tan 45\)
= 10m
In \(\Delta\) PRS,
\(\tan 30 = \frac{10}{RS} \implies RS = \frac{10}{\tan 30}\)
= \(\frac{10}\{\frac{1}{\sqrt{3}}\)
= \(10\sqrt{3}\)
PS = \(10 + 10\sqrt{3}\)
= \(10(1 + \sqrt{3}) cm\)
Similar Questions
Calculate 243\(_{six}\) – 243\(_{five}\) expressing your answer in base 10...
From the figure, calculate TH in centimeters ...
The angles of a polygon are given by 2x, 5x, x and 4x respectively. The value of x is...
If p-2g + 1 = g + 3p and p - 2 = 0, find g ...
If x2 + kx + \(\frac{16}{9}\) is a perfect square, find the value of k...
The length of an arc of a circle of radius 5cm is 4cm. Find the area of the sector ...
A pyramid is constructed on a cuboid. The figure has ...
Marks 2 3 4 5 6 7 8 9 No. of students 3 4 1 0 4 5 2 1 The table above shows the distribut...
Solve the following quadratic inequality: \(x^2 - x\) - 4 ≤ 2...