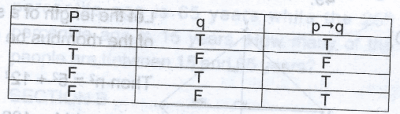
\(\frac{x}{y}\) = \(\frac{1}{4} \div \frac{3}{8}\) = \(\frac{1}{4} \times \frac{8}{3}\) = \(\frac{2}{3}\)
\(\frac{y}{z}\) = \(\frac{1}{3} \div \frac{4}{9}\) = \(\frac{1}{3} \times \frac{9}{4}\) = \(\frac{3}{4}\)
But,
x = \(\frac{2}{5}T_1\), y = \(\frac{3}{5}T_1\)
y = \(\frac{3}{7}T_2\), z = \(\frac{4}{7}T_2\)
Using y = y
\(\frac{3}{5}T_1\) = x = \(\frac{3}{7}T_2\)
\(\frac{T_1}{T_2}\) = \(\frac{3}{7}\) x \(\frac{5}{3}\) = \(\frac{15}{21}\)
\(T_1 = 15\) and \(T_2 = 21\)
Thus , x = \(\frac{2}{5}\) x 15 = 6
y = \(\frac{3}{5}\) x 15 = 9
y = \(\frac{3}{7}\) x 21 = 9
z = \(\frac{4}{7}\) x 21 = 12
Hence; x : z = 6 : 12
= 1 : 2