Line Charts Questions & Answers

26.

The following line graph gives the annual percent profit earned by a Company during the period 1995 - 2000.

Percent Profit Earned by a Company Over the Years.

%Profit = (Income - Expenditure)/Expenditure x 100

If the profit in 1999 was Rs. 4 crores, what was the profit in 2000?

Rs. 4.2 crores

Rs. 6.6 crores

Rs. 6.8 crores

Cannot be determined

View answer & explanation

Correct answer is D

From the line-graph we obtain information about the percentage profit only. To find the profit in 2000 we must have the data for the income or expenditure in 2000.

Therefore, the profit for 2000 cannot be determined.

27.

The following line graph gives the annual percent profit earned by a Company during the period 1995 - 2000.

Percent Profit Earned by a Company Over the Years.

%Profit = (Income - Expenditure)/Expenditure x 100

In which year is the expenditure minimum?

2000

1997

1996

Cannot be determined

View answer & explanation

Correct answer is D

The line-graph gives the comparison of percent profit for different years bu the comparison of the expenditures is not possible without more data.

Therefore, the year with minimum expenditure cannot be determined.

28.

The following line graph gives the annual percent profit earned by a Company during the period 1995 - 2000.

Percent Profit Earned by a Company Over the Years.

%Profit = (Income - Expenditure)/Expenditure x 100

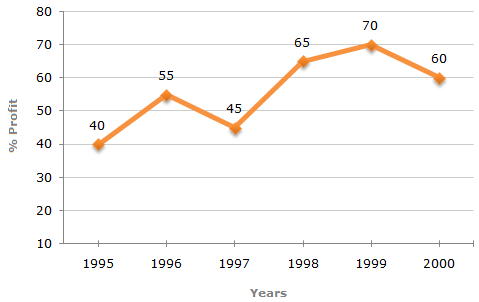
If the income in 1998 was Rs. 264 crores, what was the expenditure in 1998?

Rs. 104 crores

Rs. 145 crores

Rs. 160 crores

Rs. 185 crores

View answer & explanation

Correct answer is C

Let the expenditure is 1998 be Rs. x crores.

Then, 65 = ((264 - x)/x) x 100

=> 65/100 = (264/x) - 1

=> x = (264 x100)/165 = 160.

Therefore Expenditure in 1998 = Rs. 160 crores.

29.

The following line graph gives the annual percent profit earned by a Company during the period 1995 - 2000.

Percent Profit Earned by a Company Over the Years.

%Profit = (Income - Expenditure)/Expenditure x 100

If the expenditures in 1996 and 1999 are equal, then the approximate ratio of the income in 1996 and 1999 respectively is?

1:1

2:3

13:14

9:10

View answer & explanation

Correct answer is D

Let the expenditure in 1996 = x.

Also, let the incomes in 1996 and 1999 be I₁ and I₂ respectively.

Then, for the year 1996, we have:

55 = (I₁ - x)/x x 100 => 55/100 = I₁/x - 1 => I₁ = 155x/100 ... (i)

70 = (I₂ - x)/x x 100 => 70/100 = I₂/x - 1 => I₂ = 170x/100 ... (ii)

From (i) and (ii), we get:

I₁/I₂ = (155x/100)/(170x/100) = 155/170 ≈ 0.91/1 ≈ 9 : 10

30.

The following line graph gives the percentage of the number of candidates who qualified for an examination out of the total number of candidates who appeared for the examination over a period of seven years from 1994 to 2000.

Percentage of Candidates who Qualified to Appeared in an Examination Over the Years