In the diagram above, PQ and XY are two concentric arc; c...
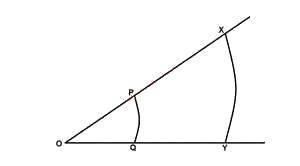
In the diagram above, PQ and XY are two concentric arc; center O, the ratio of the length of the two arc is 1:3, find the ratio of the areas of the two sectors OPQ and OXY
1:3
1:6
1:9
2:3
4:9
Correct answer is C
Let the radius of the arc PQ = r and the radius of the arc XY = R.
Length of arc PQ = θ360×2πr=1
Length of arc XY = θ360×2πR=3
Ratio of the arc = rR=360×2πθ2πθ×360×3
= 13
Ratio of their area = (13)2=19
= 1 : 9
Similar Questions
A rectangle with width 34cm and area 3 38cm2. Find the length...
If log102 = x, express log1012.5 in terms of x...
Make x the subject of the formula:y = 3x−9c4x+5d...
If U = {x : x is an integer and 1 ≤ x ≤ 20 } E1 = {x: x is a multiple of 3} E2 = {x: x is a ...
Solve the equation; 3x - 2y = 7, x + 2y = -3 ...
If f(x - 4) = x2 + 2x + 3, Find, f(2)...
If x is positive real number, find the range of values for which 13x + 12x...