In the diagram above, |PQ| = |PR| = |RS| and ∠RPS = 3...
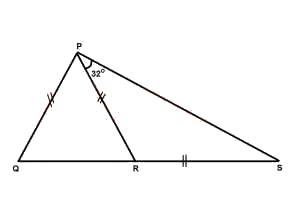
In the diagram above, |PQ| = |PR| = |RS| and ∠RPS = 32°. Find the value of ∠QPR
72o
64o
52o
32o
26o
Correct answer is C
From the figure, < PSR = 32° (base angles of an isos. triangle)
∴ < PRS = 180° - (32° + 32°) = 116° (sum of angles in a triangle)
< QRP = 180° - 116° = 64° (angle on a straight line)
< PQR = 64° (base angles of an isos. triangle)
< QPR = 180° - (64° + 64°) = 52°
Similar Questions
If y = x sin x, find \frac{\delta y}{\delta x}...
Solve the equation 10-3x-x2 = 0...
calculate the surface area of a sphere of radius 7cm [Take π = 22/7] ...
A function f(x) passes through the origin and its first derivative is 3x + 2. What is f(x)? ...
In the diagram, PTS is a tangent to the circle TQR at T. Calculate < RTS...
In ΔABC above, BC is produced to D, /AB/ = /AC/ and ∠BAC = 50o. Find ∠ACD...