In the diagram, \(\overline{MP}\) is a tangent to the circle...
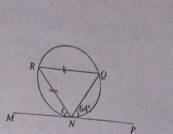
In the diagram, \(\overline{MP}\) is a tangent to the circle NQR, ∠NQR, ∠PNQ = 64 and | \(\overline{RQ}\) | = | \(\overline{RN}\) |. Find the angle market t.
A.
130°
B.
115°
C.
58°
D.
68°
Correct answer is C
Alternate segments are equal : R° = 64°
An isosceles triangle has two angles ( Q° & N° ) equal as A°
R° + A° + A° = 180°
2A°= 180 - 64
2A° = 116°
A = \(\frac{116}{2}\)
A = 58.
: Q° = 58, N° = 58 and T° = 58
As Alternate segments are equal: T = Q
Similar Questions
If PQR is a straight line with QS = QR, calculate TPQ, If QT\\SR and TQS = 3yo...
Describe the shaded portion in the diagram ...
Find the curved surface area of a cone with circular base diameter 10 cm and height 12 cm ...
Find the minimum value of y = x2 - 2x - 3...
Which of these angles can be constructed using ruler and a pair of compasses only?...