A piece of thread of length 21.4cm is used to form a sector of a circle of radius 4.2cm on a piece of cloth. Calculate, correct to the nearest degree, the angle of the sector. [Take \(\pi = \frac{22}{7}\)]
170\(^o\)
192\(^o\)
177\(^o\)
182\(^o\)
Correct answer is B
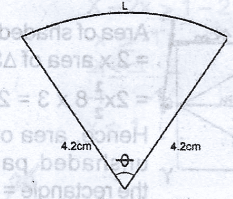
Length of arc, L = 21.4 - 2 x 4.2cm
= 21.4 - 8.4
= 13cm
But L = \(\frac{\theta}{360^o}\) x 2\(\pi r\)
i.e 13 = \(\frac{\theta}{360^o}\) x 2 x \(\frac{22}{7}\) x 4.2
= 13 x 360\(^o\) x 7
= \(\theta\) x 2 x 22 x 4.2
\(\theta\) = \(\frac{13 \times 360^o \times 7}{44 \times 4.2}\)
= \(\approx\) 177.27\(^o\)
\(\approx\) 177\(^o\) (to the nearest degree)
Similar Questions
Solve the simultaneous equation: x+y=2 and 3x-2y=1 ...
Evaluate log\(_2\) 8 – log\(_3\) \(\frac{1}{9}\)...
For a class of 30 students, the scores in a Mathematics test out of 10 marks were as follows; 4,5...
If y varies directly as the square root of x and y = 3 when x&nbs...
Evaluate ∫\(^{\pi}_{2}\)(sec2 x - tan2x)dx...
Evaluate \(\left(\frac{81}{16}\right)^{\frac{-1}{4}}\times 2^{-1}\) ...
The diagonals of a rhombus are 16 cm and 12 cm find the length of the side. ...