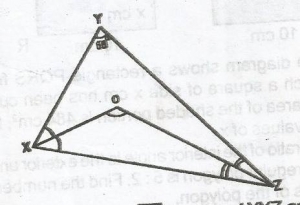
$In the diagram, $\bar{OX}$ bisects < YXZ and $\bar{OZ}$ bisects < YZX. If < XYZ = 68o, calculate the value of < XOZ$

In the diagram, $\bar{OX}$ bisects < YXZ and $\bar{OZ}$ bisects < YZX. If < XYZ = 68^o, calculate the value of < XOZ

68^o

72^o

112^o

124^o

View answer & explanation

Correct answer is D

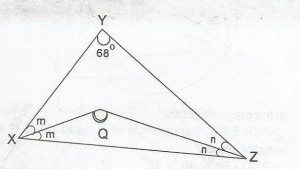
In $\Delta$ XYZ, 2m + 2n + 68^o = 180^o

2(m + n) + 68^o = 180^o...(1)

in $\Delta$ XOZ, m + n + q = 180^o ...(2)

(m + n) = 180^o - q...(3)

substituting 180^o - q for (m + n) in (1) gives

2(180^o - q) + 68^o = 180^o

360^o - 2q = 180^o - 68^o

360^o - 2q = 112^o

360^o - 112^o = 2q

248^o = 2q

q = $\frac{248^o}{2}$

= 124^o

hence, < XOZ = 124^o

See all Mathematics questions & answers

See more WAEC questions & answers

In the diagram, \(\bar{OX}\) bisects < YXZ and \(\bar{OZ}\) bisects < YZX. If < XYZ = 68^o, calculate the value of < XOZ

Aptitude Tests

In the diagram, \(\bar{OX}\) bisects < YXZ and \(\bar{OZ}\) bisects < YZX. If < XYZ = 68o, calculate the value of < XOZ

Aptitude Tests

In the diagram, \(\bar{OX}\) bisects < YXZ and \(\bar{OZ}\) bisects < YZX. If < XYZ = 68^o, calculate the value of < XOZ