Evaluate (sin45º + sin30º ) in...
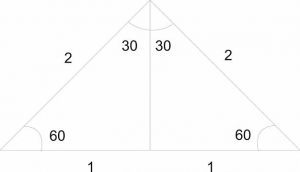
Evaluate (sin45º + sin30º ) in surd form
A.
√32√2
B.
√3 − 12
C.
12√2
D.
1 + √22
Correct answer is D
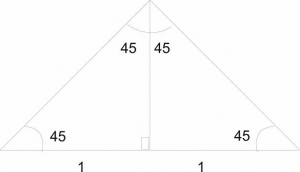
hypotenuse
sin = 12
sin45=1√2
= 22
∴ (sin45 + sin30)
= 1√2+12
= √22 + 12
= √2+12
= 1+√22
Similar Questions
If a binary operation * is defined by x * y = x + 2y, find 2 * (3 * 4)...
If M(4, q) is the mid-point of the line joining L(p, -2) and N(q, p). Find the values of p and q ...
Which of the following is not necessarily true of a rectangle? ...
If the mean of 2, 5, (x+1), (x+2), 7 and 9 is 6. Find the median ...
Solve the following equation: 2(2r−1) - 53 = \(\frac{1}{(r + ...
Which of the following pairs of inequalities is represented on the number line? ...