In the diagram, 0 is the centre of the circle. Find the v...
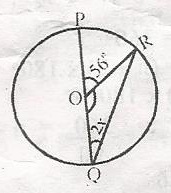
In the diagram, 0 is the centre of the circle. Find the value x
34
29
17
14
Correct answer is D
POQ in a straight line
Hence, < POQ + < QOR = 180o
56o + < QOR = 180o
< QOR = 180o - 56o
= 124o
Now, in \(\bigtriangleup\) QOR OR = OQ = Radius
< ORQ = < OQR = 2x (Base angles of an Isosceles \(\bigtriangleup\))
2x + 124 + 2x = 180o
4x + 124 = 180
4x = 180 - 124
4x = 56
x = \(\frac{56}{4}\)
x = 14o
Similar Questions
Make t the subject of k = \(m \sqrt \frac{t-p}{r}\)...
If (g(y)) = \(\frac{y - 3}{11}\) + \(\frac{11}{y^2 - 9}\). what is g(y + 3)?...
Find the roots of the equations: \(3m^2 - 2m - 65 = 0\)...
Find the distance between the points C(2, 2) and D(5, 6)....
Evaluate \(\frac{8^{\frac{1}{3}} \times 5^{\frac{2}{3}}}{10^{\frac{2}{3}}}\) ...
Find the equation of the locus of a point P(x,y) which is equidistant from Q(0,0) and R(2,1). ...