In the diagram, PX is a tangent to the circle and RST is ...
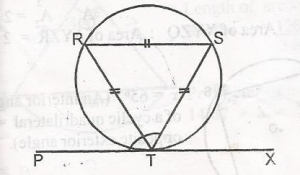
In the diagram, PX is a tangent to the circle and RST is an equilateral triangle. Calculate < PTS
60o
90o
120o
150o
Correct answer is C
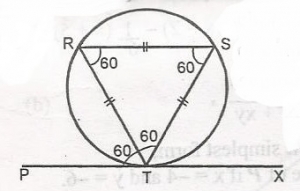
△ RST is equilateral triangle, hence
< TRS = < RTS = < RSt = 60o
But < PTR = 60o(Angle between a chord and a tangent at the point of contact = Angle in the alt. segment). From the diagram < PTS = < PTR + < RTS
= 60o + 60o = 120o
Similar Questions
Evaluate xy2−x2yx2−xy1 When x = -2 and y = 3...
In the diagram, |QR| = 5cm, PQR = 60<sup>o</sup> and PSR = 45<sup>o</sup>. F...
Solve for a positive number x such that 2(x3−x2−2x)=1...
The roots of a quadratic equation are 43 and -37. Find the equation...
Evaluate (0.142×0.275)7(0.02) to 3 decimal places. ...
The length, breadth and height of a cuboid are 8cm, 712cm and 612 cm respe...