Abstract Analytical Reasoning Questions & Answers - Page 4

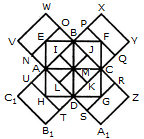
The figure may be labelled as shown.

The squares composed of two components each are BJMI, CKMJ, DLMK and AIML i.e. 4 in number.

The squares composed of three components each are EBMA, BFCM, MCGD and AMDH i.e. 4 in number.

The squares composed of four components each are VWBA, XYCB, ZA1DC and B1C1AD i.e. 4 in number.

The squares composed of seven components each are NOJL, PQKI, RSLJ and TUIK i.e. 4 in number.

There is only one square i.e. ABCD composed of eight components.

There is only one square i.e. EFGH composed of twelve components.

Total number of squares in the figure = 4 + 4 + 4 + 4 + 1 + 1 = 18.

The figure may be labelled as shown.

Triangles:

The simplest triangles are KJN, KJO, CNB, OEF, JIL, JIM, BLA and MFG i.e. 8 in number.

The triangles composed of two components each are CDJ, EDJ, NKO, JLM, JAH and JGH i.e. 6 in number.

The triangles composed of three components each are BKI, FKI, CJA and EJG i.e. 4 in number.

The triangles composed of four components each are CDE and AJG i.e. 2 in number.

The only triangle composed of six components is BKF.

Thus, there are 8 + 6 + 4 + 2 + 1 = 21 triangles in the given figure.

Parallelograms :

The simplest parallelograms are NJLB and JOFM i.e. 2 in number.

The parallelograms composed of two components each are CDKB, DEFK, BIHA and IFGH i.e.4 in number.

The parallelograms composed of three components each are BKJA, KFGJ, CJIB and JEFI i.e.4 in number.

There is only one parallelogram i.e. BFGA composed of four components.

The parallelograms composed of five components each are CDJA, DEGJ, CJHA and JEGH i.e.4 in number.

The only parallelogram composed of six components is CEFB.

The only parallelogram composed of ten components is CEGA.

Thus, there are 2 + 4 + 4 + 1 + 4+ 1 + 1 = 17 parallelograms in the given figure.

(Here note that the squares and rectangles are also counted amongst the parallelograms).

The figure may be labelled as shown.

The squares composed of two components each are BNQM, CORN, DPSO, MQTL, NRUQ, OSVR, PFWS, QUJT, RVIU and SWHV i.e. 10 in number.

The squares composed of four components each are ABQL, BCRQ, CDSR, DEFS, LQJK, QRIJ, RSHI and SFGH i.e. 8 in number.

The squares composed of eight components each are BRJL, CSIQ and DFHR i.e. 3 in number.

The squares composed of sixteen components each are ACIK, BDHJ and CEGI i.e. 3 in number.

Thus, there are 10 + 8 + 3 + 3 = 24 squares in the figure.

The figure may be labelled as shown.

Triangles :

The simplest triangles are BPN, PNE, ABM, EFG, MLK, GHI, QRO, RSO, STO and QTO i.e. 10 in number.

The triangles composed of two components each are BPE, TQR, QRS, RST and STQ i.e. 5 in number.

The triangles composed of three components each are MPO and GPO i.e. 2 in number.

The triangles composed of six components each are LPJ, HPJ and MPG i.e. 3 in number.

There is only one triangle LPH composed of twelve components.

Total number of triangles in the figure = 10 + 5 - 2 + 3 + 1 = 21.

Squares :

The squares composed of two components each are KJOM and JIGQ i.e. 2 in number.

The squares composed of three components each are ANOM, NFGO and CDEB i.e.3 in number.

There is only one square i.e. QRST composed of four components.

There is only one square i.e. AFIK composed of ten components.

Total number of squares in the figure = 2 + 3 + 1 + 1 = 7.

The figure may be labelled as shown.

We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.

The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number.

The squares composed of four simple squares are ACIG and DFLJ i.e. 2 in number.

Thus, 6 + 2 = 8 squares will be formed.