Processing math: 100%

Home / Aptitude Tests / Mathematics / The diagram shows a ...

The diagram shows a trapezium inscribed in a semi-circle....

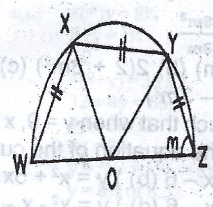
The diagram shows a trapezium inscribed in a semi-circle. If O is the mid-point of WZ and |WX| = |XY| = |YZ|, calculate the value of m

The diagram shows a trapezium inscribed in a semi-circle. If O is the mid-point of WZ and |WX| = |XY| = |YZ|, calculate the value of m

A.

90 $^o$

B.

60 $^o$

C.

45 $^o$

D.

30 $^o$

View answer & explanation

Correct answer is B

In the diagram, < WOZ = 180 $^o$ (angle on a straight line)

< WOX = < XOY = < YOZ

(|WX| = |XY| = |YZ|)

$\frac{180^o}{3}$ = 60 $^o$

= 60 $^o$

M + m =2m (base angles of isosceles $\bigtriangleup$ , |OY| and |OZ| are radii)

< YOZ + 2m (base angles of a $\bigtriangleup$ )

60 $^o$ + 2m = 180 $^o$ (sum of a $\bigtriangleup$ )

60 $^o$ + 2m = 180 $^o$

2m = 180 $^o$ - 60 $^o$

2m = 120 $^o$

m = $\frac{120^o}{2}$

= 60 $^o$

See all Mathematics questions & answers

See more WAEC questions & answers

Similar Questions

Which of the following is a root of the equation x $^2$ +6x = 0?...

If log520 = x, find x...

A school boy lying on the ground 30m away from the foot of a water tank towel observes that the angl...

In a class of 30 students, the marks scored in an examination are displayed in the histogram. What p...

The angle of elevation of the top of a tree from a point 27m away and on the same horizontal ground ...

Bola sold an article for N6,900.00 and made a profit of 15%. If he sold it for N6,600.00 he would ma...

In the diagram, △XYZ is produced to T. if |XY| = |ZY| and ∠XYT = 40°, find ...

In the diagram, < PSR = 220o, < SPQ = 58o and < PQR = 41o. Calculate the obtuse angle QRS....

In one and a half hours, the minute hand of a clock rotates through an angle of ...

Points X and Y are respectively 12m North and 5m east of point Z. Calculate XY ...

Aptitude Tests

Situational Judgement Questions and Answers

Typing Speed and Accuracy Test

Abstract Reasoning Questions and Answers

Microsoft Office Questions and Answers

Logical Reasoning Questions and Answers

Numerical Reasoning Questions and Answers

Verbal Reasoning Questions and Answers

Puzzles Questions and Answers

Nigeria General Knowledge Questions and Answers

Spatial Reasoning Questions and Answers

Data Interpretation Questions and Answers

Quantitative Reasoning Questions and Answers

Personality Test

View latest jobs in Nigeria today