The ratio of the exterior angle to the interior angle of ...
The ratio of the exterior angle to the interior angle of a regular polygon is 1:11. How many sides has the polygon?
30
24
18
12
Correct answer is B
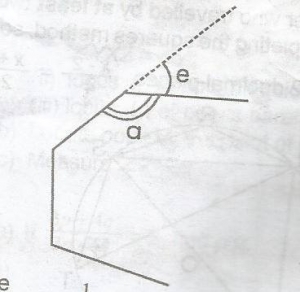
Let a represent an interior angle; e represent an exterior angle. A section of the polygon is down in the diagram.
ea = l11 given
a = 11e
a + e = 180o(angles on a straight line)
11e + e = 180o
12e = 180o
e = 180o12
= 15o
Hence, number of sides
= \frac{360^o}{\tect{size of one exterior angle}
= 360o14o
= 24
Similar Questions
I am x years old and my brother is 3 years older. How old was my brother last year? ...
If x > 0, find the range of number x-3, 3x+2,x-1, 4x, 2x-1, x-2, 2x-2, 3x and 3x+1 ...
Evaluate 2log39×log381−2log5625...
If 12x + 2y = 3 and 32x and 32x - 2y = 1, find (x + y)...
The graph represents the relation y = x2 - 3x - 3. What is the equation of the line of symmetry...