The velocity ratio of an inclined plane where angle of in...
The velocity ratio of an inclined plane where angle of inclination in θ is
Sinθ
Cosθ
Tanθ
\(\frac{1}{\sin \theta}\)
Correct answer is D
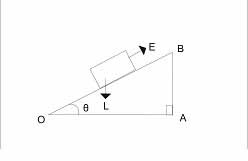
Consider an inclined plane shown below, as the effort moves along OB, the load moves is lifted up through a vertical height AB
V.R = \(\frac{\text{distance moved by effort}}{\text{distance moved by load}}\) = \(\frac{OB}{AB}\)
But Sinθ = \(\frac{opp}{hyp}\) = \(\frac{AB}{OB}\)
therefore; = \(\frac{OB}{AB}\) = \(\frac{1}{\sin \theta}\)
Similar Questions
If silicon is doped with phosphorus, what type of semiconductor material will be formed? ...
When left in a freezer, a bottle full of water cracks on freezing into ice because of the ...
Which of the following statements about the atom is/are correct? I. Energy is needed to remove el...
Which of the following statements is true of the diagram shown above? ...
The value of F in the figure above when in equilibrium is ...
Which of the following instruments can be used to measure current in an a.c circuit? ...