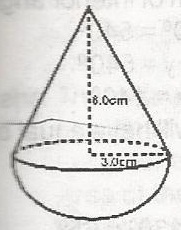
In the figure, a solid consists of a hemisphere surmounted by a right circular cone, with radius 3.0cm and height 6.0cm. Find the volume of the solid

Similar Questions

If the 3rd and the 5th terms of an A.P are 6 and 10 respectively, find the 1st term and the common d...

In the diagram above, find x correct to the nearest degree ...

Factorize a2x - b2y - b2x + a2y ...

Convert the decimal number 89 to a binary number ...

If it is given that 5x + 1 + 5x = 150, then the value of x is equal to...

S = {1, 2, 3, 4, 5, 6}, T = {2,4,5,7} and R = {1,4, 5}, and (S∩T) ∪ R ...

Simplify $7\frac{1}{2}-\left(2\frac{1}{2}+3\right)\div16\frac{1}{2}$and correct your answer to the...

Evaluate ($\frac{1}{343}$)$^{\frac{1}{3}}$ + (64)$^{-\frac{1}{3}}$ - $\frac{4}{9}$\(^{-\frac...

An arc subtends an angle of 50o at the center of circle of radius 6cm. Calculate the area of the sec...

A trader realizes 10x - x$^2$ naira profit from the sale of x bags on corn. How many bags will giv...