In the figure, GHIJKLMN is a cube of side a. Find the len...
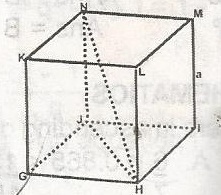
In the figure, GHIJKLMN is a cube of side a. Find the length of HN.
√3a
3a
3a2
a√2
a√3
Correct answer is E
HJ2 = a2 + a2 = 2a2
HJ = √2a2=a√2
HN2 = a2 + (a√2)2 = a2 + 2a2 = 3a2
HN = √3a2
= a√3cm
Similar Questions
The area of a trapezium is 200 cm2. Its parallel sides are in the ratio 2 : 3 and the perpendic...
Find the gradient of the line passing through the points P(1, 1) and Q(2, 5). ...
In the figure, PQRS is a rectangle. If the shaded area is 72 sq. cm, find h. ...
In triangle PQR, q = 8 cm, r = 6 cm and cos P = 112. Calculate the value of p....
If 2x2 - kx - 12 is divisible by x-4, Find the value of k. ...
If x2+15x+50=ax2+bx+c=0. Which of the following statement is not true?...
Use the graph to answer the Question below What are the roots of the equation x2 + 3x - 4 = 0?...