Processing math: 100%

Home / Aptitude Tests / Mathematics / Find the area of the...

Find the area of the shaded portion of the semicircular f...

Find the area of the shaded portion of the semicircular figure.

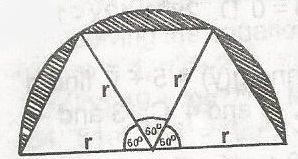
Find the area of the shaded portion of the semicircular figure.

A.

$\frac{r^2}{4}(4 \pi - 3 \sqrt{3})$

B.

$\frac{r^2}{4}(2 \pi - 3 \sqrt{3})$

C.

$\frac{1}{2}r^2 \pi$

D.

$\frac{1}{8}r^2 \sqrt{3}$

E.

$\frac{r^2}{4}(4 \pi - 3 \sqrt{3})$

View answer & explanation

Correct answer is B

A_sector = $\frac{60}{360} \times \pi r^2$

= $\frac{1}{6} \pi r^2$

A_{$\bigtriangleup$} = $\frac{1}{2}r^2 \sin 60^o$

$\frac{1}{2} r^2 \times \frac{\sqrt{3}}{2} = \frac{r^2\sqrt{3}}{4}$

A_{$\text{shaded portion}$} = A_sector -
A_{$\bigtriangleup$}

= ( $\frac{1}{6} \pi r^2 - \frac{r^2\sqrt{3}}{4})^3$

= $\frac{\pi r^2}{2} - \frac{3r^2\sqrt{3}}{4}$

= $\frac{r^2}{4}(2 \pi - 3 \sqrt{3})$

See all Mathematics questions & answers

See more JAMB questions & answers

Similar Questions

The shaded portion in the venn diagram is ...

What is the difference in longitude between P (lat. 50°N. long. 50°W) and Q (lat.50°N, l...

Find the equation of a line parallel to y = -4x + 2 passing through (2,3) ...

A straight line y = mx meets the curve y = x2 - 12x + 40 in two distinct points. If one of them is (...

the graph above is a sketch of ...

Make S the subject of the relation p = s + $\frac{sm^2}{nr}$ ...

Factorize 2x $^2$ - 21x + 45...

The pie chart above shows the distribution of subjects offered by students in SSS III level. If 80 s...

If p varies inversely as the cube of q and q varies directly as the square of r, what is the relatio...

If the volume of a cube is (8 x 103)cm $^3$ , what is the surface area the cube?...

Aptitude Tests

Quantitative Reasoning Questions and Answers

Spatial Reasoning Questions and Answers

Nigeria General Knowledge Questions and Answers

Typing Speed and Accuracy Test

Logical Reasoning Questions and Answers

Personality Test

Abstract Reasoning Questions and Answers

Numerical Reasoning Questions and Answers

Data Interpretation Questions and Answers

Situational Judgement Questions and Answers

Microsoft Office Questions and Answers

Verbal Reasoning Questions and Answers

Puzzles Questions and Answers

View latest jobs in Nigeria today