In the diagram O and O' are the centres of the c...
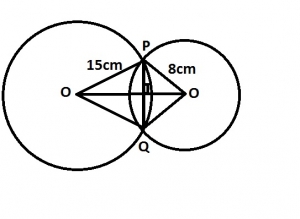
In the diagram O and O' are the centres of the circles radii 15cm and 8cm respectively. If PQ = 12cm, find |OO'|.
8.46cm
19.04cm
20.81cm
26.16cm
Correct answer is B
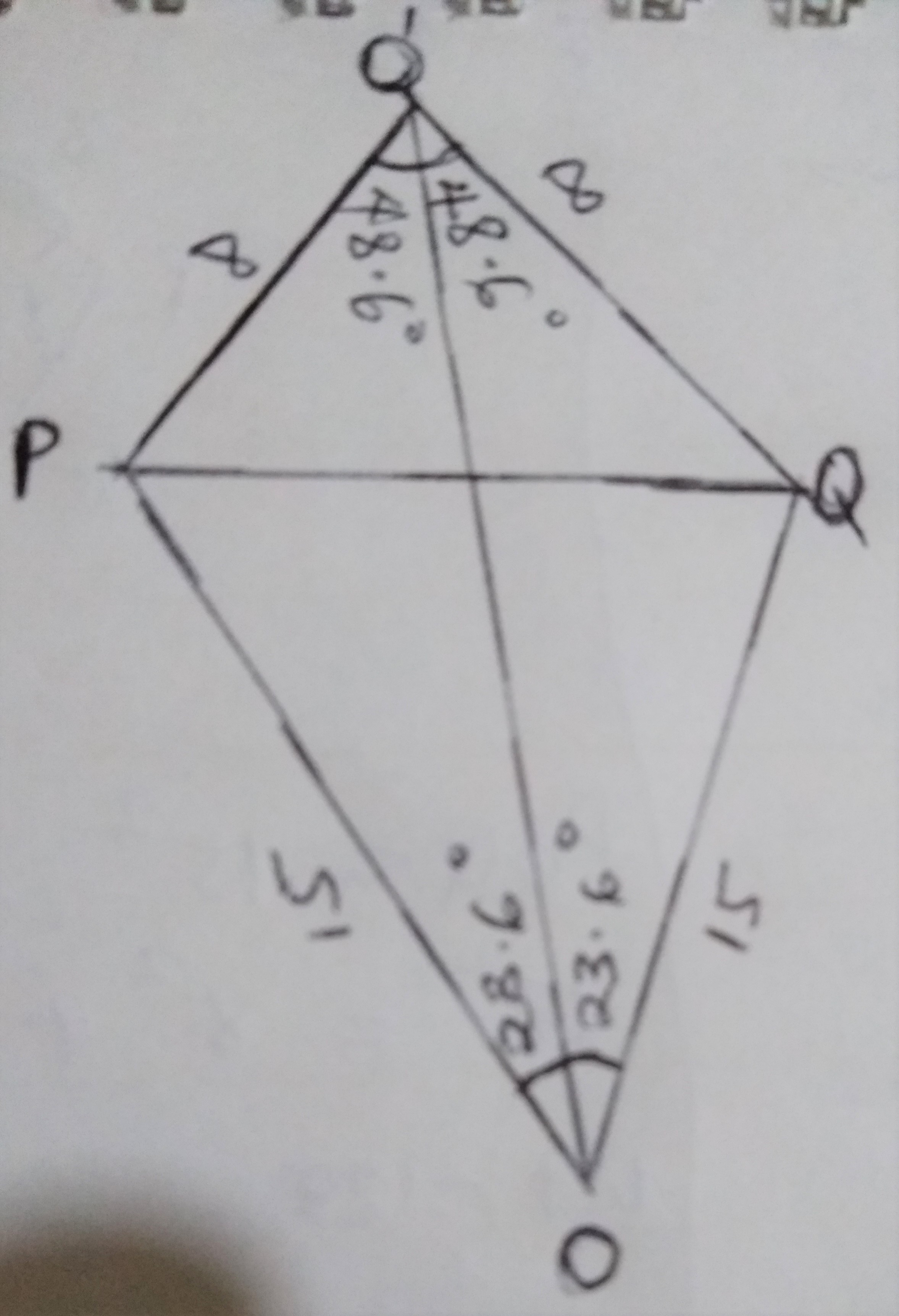
In Δ POQ,
122=152+152−2(15)(15)cos<POQ
144=450−450cos<POQ
450cos<POQ=450−144=306
cos<POQ=306450=0.68
< POQ = 47.2°
In \Delta PO'Q,
12^2 = 8^2 + 8^2 - 2(8)(8) \cos <PO'Q
144 - 128 = -128 \cos < PO'Q
\cos < PO'Q = - 0.125
< PO'Q = 97.2°
In \Delta POQ,
\cos 23.6 = \frac{x}{15}
x = 15 \times \cos 23.6
= 13.75 cm
In \Delta PO'Q,
\cos 48.6 = \frac{y}{8}
y = 8 \times \cos 48.6
= 5.29 cm
\therefore OO' = x + y = 13.75 + 5.29
= 19.04 cm
Similar Questions
If 27x = 9y. Find the value of \frac{x}{y}...
Find the median of the set of numbers 110, 116, 113, 119, 118, 127, 118, 117, 113 ...
Find the sum to infinity of the following sequence \(1, \frac{9}{10}, (\frac{9}{10})^{2}, ...
A solid hemisphere has a radius of 7 cm. Find the total surface area. ...
Oke deposited N800.00 in the bank at the rate of 12\frac{1}{2}% simple interest. After some time...