Evaluate \(\frac{2\sin 30 + 5\tan 60}{\sin 60}\), leaving your answer in surd form.
\(\frac{2\sqrt{3}}{3} + 10\)
\(\frac{3\sqrt{2} - 1}{5}\)
\(\frac{3\sqrt{2} + 1}{5}\)
\(\frac{2\sqrt{3}}{3} - 10\)
Correct answer is A
\(\frac{2\sin 30 + 5\tan 60}{\sin 60}\)
\(\sin 30 = \frac{1}{2}; \tan 60 = \sqrt{3}; \sin 60 = \frac{\sqrt{3}}{2}\)
\(\therefore \frac{2\sin 30 + 5\tan 60}{\sin 60} = \frac{2(\frac{1}{2}) + 5(\sqrt{3})}{\frac{\sqrt{3}}{2}}\)\)
= \(\frac{1 + 5\sqrt{3}}{\frac{\sqrt{3}}{2}}\)
= \(\frac{2(1 + 5\sqrt{3})}{\sqrt{3}}\)
= \(\frac{2 + 10\sqrt{3}}{\sqrt{3}}\)
Rationalizing, we get
= \(\frac{2\sqrt{3} + 30}{3}\)
= \(\frac{2}{3} \sqrt{3} + 10\)
If \(\sin x = \frac{4}{5}\), find \(\frac{1 + \cot^2 x}{\csc^2 x - 1}\).
\(\frac{13}{2}\)
\(\frac{25}{9}\)
\(\frac{3}{13}\)
\(\frac{4}{11}\)
Correct answer is B
\(\sin x = \frac{opp}{Hyp} = \frac{4}{5}\)
5\(^2\) = 4\(^2\) + adj\(^2\)
adj\(^2\) = 25 - 16 = 9
adj = \(\sqrt{9}\) = 3
\(\tan x = \frac{4}{3}\)
\(\cot x = \frac{1}{\frac{4}{3}} = \frac{3}{4}\)
\(\cot^2 x = (\frac{3}{4})^2 = \frac{9}{16}\)
\(\csc x = \frac{1}{\sin x}\)
= \(\frac{1}{\frac{4}{5}} = \frac{5}{4}\)
\(\csc^2 x = (\frac{5}{4})^2 = \frac{25}{16}\)
\(\therefore \frac{1 + \cot^2 x}{\csc^2 x - 1} = \frac{1 + \frac{9}{16}}{\frac{25}{16} - 1}\)
= \(\frac{25}{16} \div \frac{9}{16}\)
= \(\frac{25}{9}\)
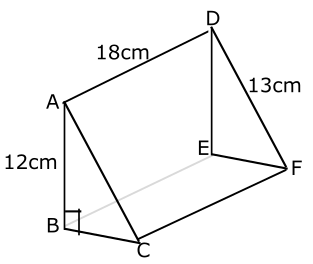
394 cm\(^3\)
425 cm\(^3\)
268 cm\(^3\)
540 cm\(^3\)
Correct answer is D
|AC| = |DF| = 13 cm
Using Pythagoras theorem,
|AC|\(^2\) = |AB|\(^2\) + |BC|\(^2\)
13\(^2\) = 12\(^2\) + |BC|\(^2\)
|BC|\(^2\) = 169 - 144 = 25
|BC| = \(\sqrt{25}\)
= 5 cm
Volume of triangular prism = \(\frac{1}{2} \times base \times length \times height\)
= \(\frac{1}{2} \times 5 \times 12 \times 18\)
= 540 cm\(^3\)
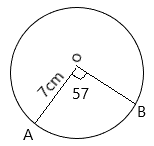
In the circle above, with centre O and radius 7 cm. Find the length of the arc AB, when < AOB = 57°
5.32 cm
4.39 cm
7.33 cm
6.97 cm
Correct answer is D
Length of arc = \(\frac{\theta}{360°} \times 2 \pi r\)
= \(\frac{57}{360} \times 2 \times \frac{22}{7} \times 7\)
= 6.97 cm
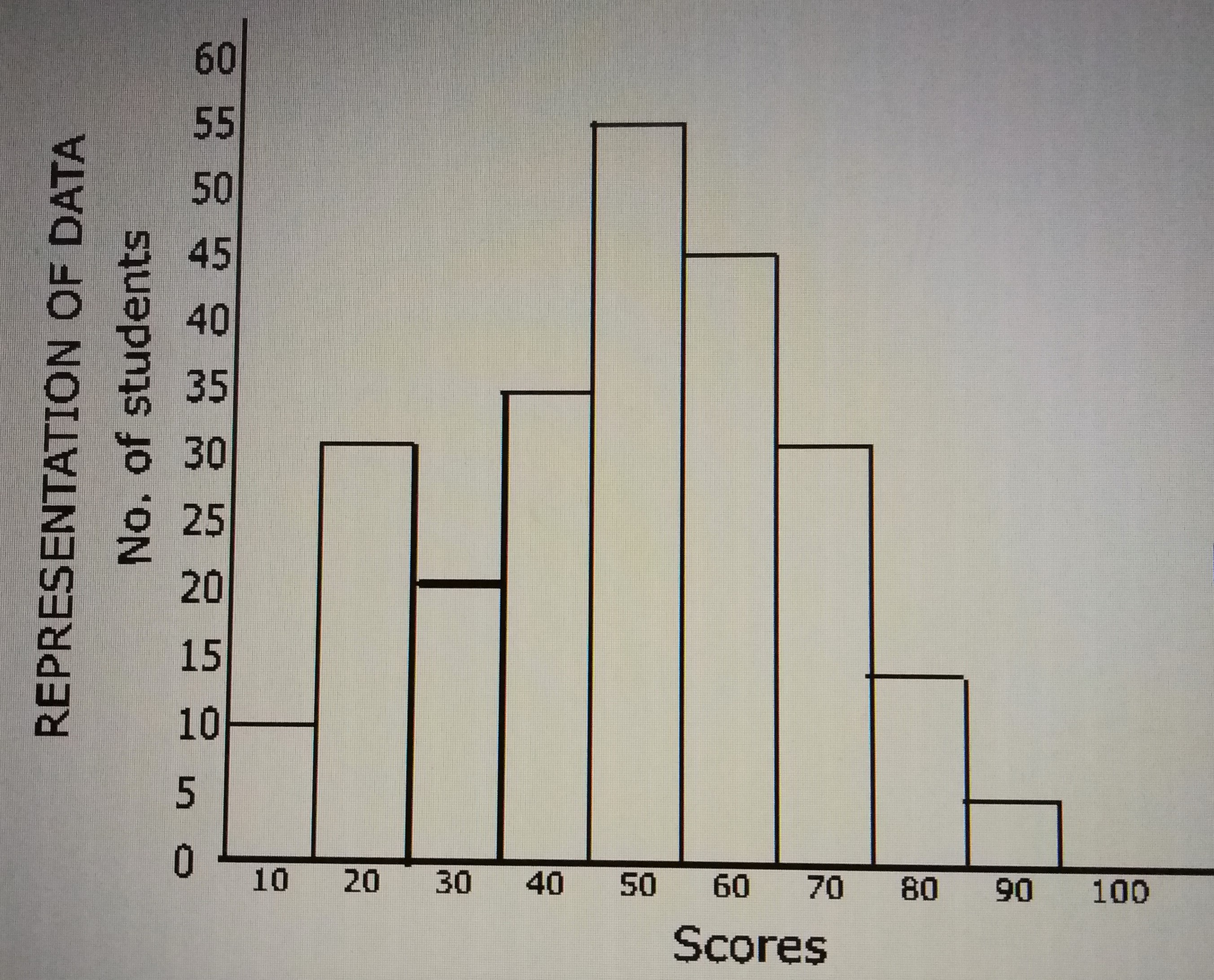
100
79
150
90
Correct answer is C
Number of students that scored above 40 = 55 + 45 + 30 + 15 + 5 = 150 students.
JAMB Subjects
Aptitude Tests